
编辑导语:我们都知道产品推出和活动策划,最终是以用户数据量来检验是否成功,那么在正式推出前是需要提前预判效果。那么本文提出生物学上的对照实验方法“AB实验”,本文主要介绍AB实验的应用场景、统计学原理以及常用的分层机制及其原理,值得阅读学习。

考虑以下两个场景:
场景1:过年前3天,产品X依据业务经验信心满满上线新版首页。全量铺开一天后,DAU环比大幅下跌。下跌原因是新版首页还是过年期间流量自然下跌?新版首页到底好还是不好?
场景2:算法X与算法Y在同一天推全A、B两个策略,全量上线后,成交效率直线上升。两人为成交效率贡献度吵得不可开交。
以上两种问题都可以通过AB实验来解决。AB实验源于生物学中的对照实验,核心原理是通过随机分流创造一个实验环境,使得实验组与对照组的唯一差异是待检验的部分,从而观察到的组间差异可以确认与待检验因素有因果关系。
AB实验核心价值能用对比分析、降风险、提效率来概括。通过AB测试,能够准确、定量的实现小成本试错以及高效率迭代。
一、AB实验原理AB实验核心统计学原理是通过假设检验,来校验实验组与对照组的样本均值差相对样本方差来说是否足够大,是否能确定地说实验组与对照组样本均值的差异是稳定的而非波动导致。
一个典型的AB实验会经历设定预期、设定最小样本量、AA校验、AB检验共4个流程。
1. 设定预期这个阶段比较简单,直接给出包含指标、涨跌幅的预期即可,例如GMV+0.5%,不喜欢该商品点击率 -3%等。
2. 设定最小样本量首先引入以下两个统计学概念:
第一类错误(α):原假设为真时拒绝原假设的概率
第二类错误(β):原假设为假时接收原假设的概率
原假设一般指不符合预期的情况,备择假设则是期望发生的情况,例如实验期望GMV涨,则H0:GMV_diff=0、H1:GMV_diff>0。通俗的说:第一类错误(α)指实验结果不符合预期但你以为它符合预期,拒绝了真的原假设(拒真);第二类错误(β)指实验结果符合预期但你以为它不符合预期,接受了错误的原假设(受伪)。
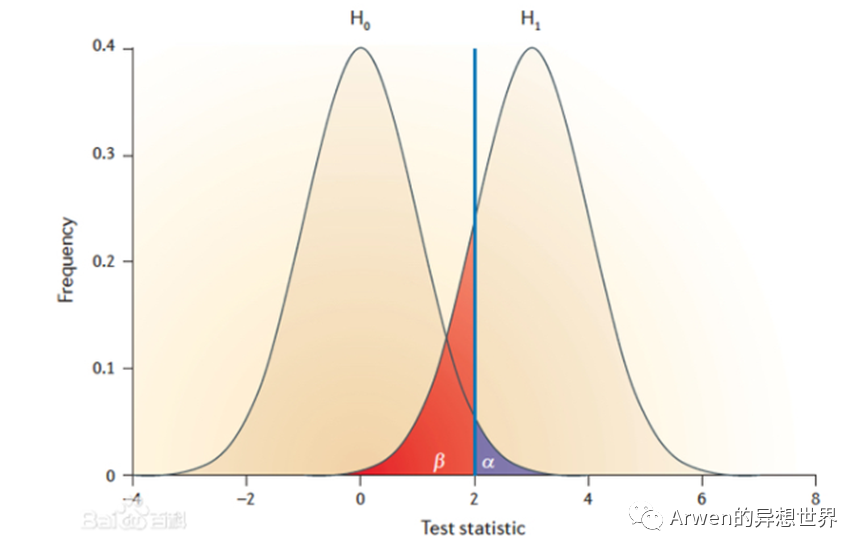
图源:百度百科
样本量越小,样本方差越大,则一二类错误概率越大,因此理论上实验样本量越大越好。但在实践中总会期望用最小的样本量进行试验:1)试错成本:引发下跌的实验开20%流量与5%流量实验成本显然不同 2)效率:单个实验流量越大,能同时进行的实验数也就越少,单个实验流量过大会影响业务整体迭代效率。因此需要找到一个平衡的样本量能同时兼顾成本/效率以及准确性。
通常在实际业务中,第二类错误后果相对较为严重,因为第一类错误导致全量无效策略,第二类错误则直接错失上涨机会。因此,一般使用power=1-β来确定实验最小样本量。
以单边检验为例(实践中单边检验较多,双侧检验可以尝试自行推导),假设实验预期目标diff为△,d是不拒绝H0的临界值。
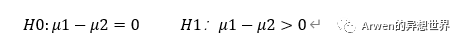
得出:

计算最小样本量可能是一件相对麻烦的事。通常需要将不同得到n1、n2及其对应的s1和s2带入公式中反复尝试。
3. AA测试AB试验开始前,一般会对空白的实验组和对照组进行AA测试。AA实验应该大概率通过检验,否则一定是埋点、分流、数据其中某些环节存在问题。除此之外,AA测试还能有效预防以下两种情况:
a.历史实验对用户的延迟效应:之前的实验影响可能持续到实验下线后,从而造成流量天然不平。
b.少数情况下样本正态性不一定成立,需要通过AA测试来发现这一问题。
AA测试具体统计学原理与AB测试一样,在AB测试部分详细展开
4. AB测试总共有以下3个步骤,依然以单侧检验为例。
Step-1:假设
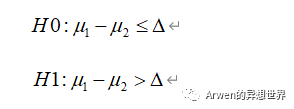
Step-2:构造统计量
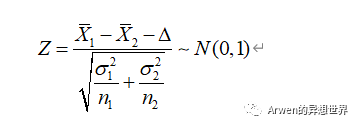
其中,△为实验预期
Step-3:比较临界值并做出决策
单侧检验中,
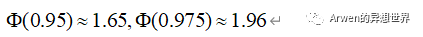
当Step2中的Z值小于临界值时,不拒绝原假设,认为实验没有显著效应;当Step2中的Z值大于临界值时,拒绝原假设,认为实验存在显著效应,实验成功!
Step-4:置信区间
虽然Step-3中已经能够说明实验有效,但还需进一步计算置信区间,增加实验结论携带的有效信息。
统计学意义是:实验的真实效果有1-α的概率落在置信区间内
二、分层机制如果一个实验需要10%流量的实验组与10%流量的对照组,那么在最理想情况下,单个层最多能同时运行9个实验。当以上实验效率不满足业务发展需要时,就应该考虑实验分层了。
分桶可以理解为纵向切分流量,桶与桶之前互不重叠;分层则是横向切分流量,层与层之间相互正交,一个用户同时属于多个不用层。有点类似城市中修建平房不能满足居住需求时,居住建筑就会变得越来越高,层数越来越多。
完全的正交使得layer1上的实验流量被均匀分配到layer2中,对layer2上的流量来说,实验与对照的唯一差距仍然是layer2实验中待检验的部分,实验环境仍然成立。
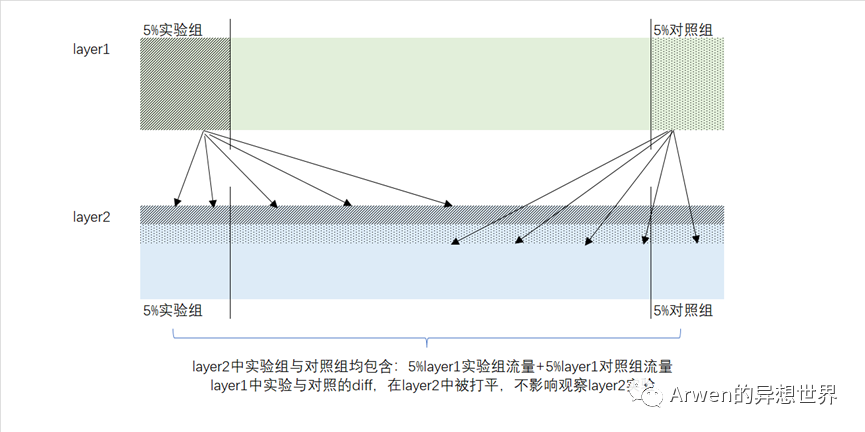
层与层之间完全正交的前提是用户在两个层上完全被随机打散,即两个层相互独立。用哈希算法来解决这个问题就变得非常简单。只要盐值变化,哈希算法就能给出不同的打散结果。常用的哈希算法有MD5和CRC两种,具体算法与数据侧关系不大,不做详细展开。注意使用CRC算法时需要注意不同层的盐值不应取用类似layer1、layer2、layer3……比较相似的名称。如下图所示,CRC是典型的伪随机算法,当打散seeds(盐值)过于相似时,层与层之间并不相互独立。
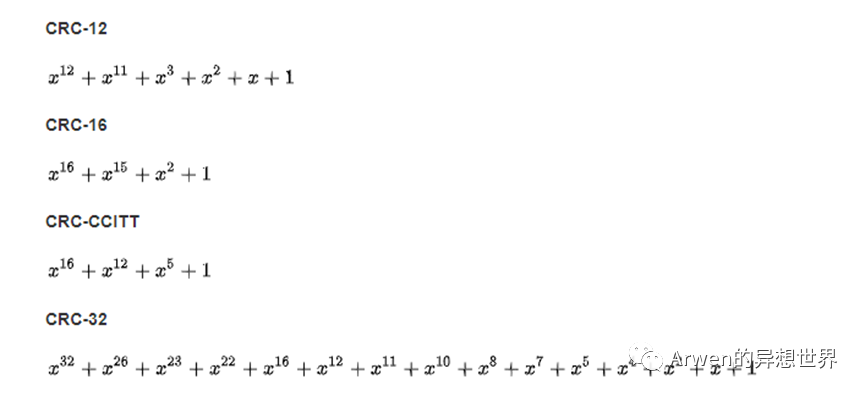
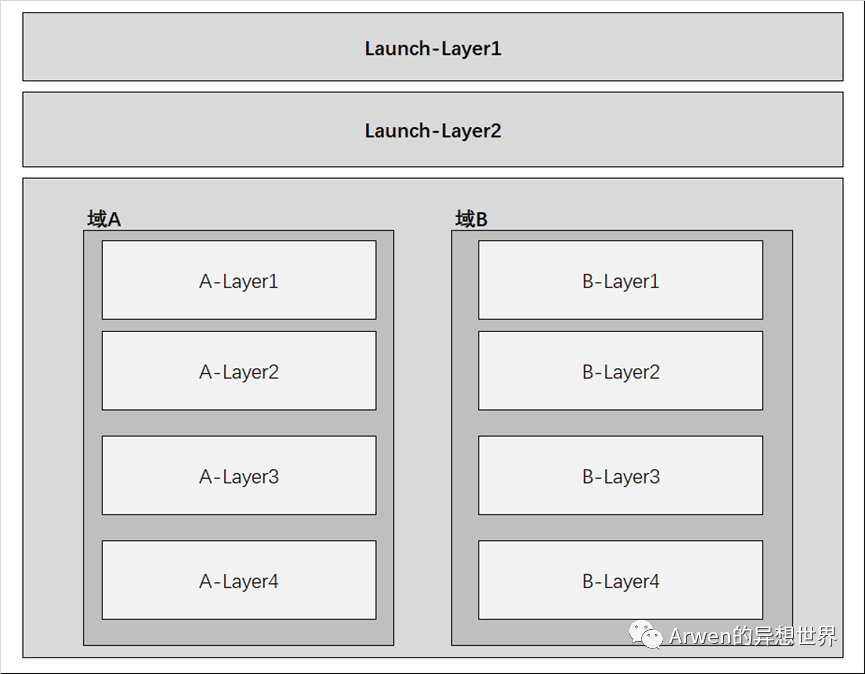
在层之外还有域的划分(domain),域的划分更适合独立实验,域和域之间也不会相互影响。发布层(Launch-Layer)则一般用来观察n个策略的打包效果,确定本次集成发版的最终影响。
本篇主要介绍AB实验的应用场景、统计学原理以及常用的分层机制及其原理。如果认真读懂本篇,常规情境下的AB实验应该都能搞定。
但在实践中有很多情况会偏离常规情景,例如实验局部生效、分析单元与随机单元不一致、多重检验问题、正态假设不满足等。后续实践篇中会逐步探讨并介绍以上问题的解决方法。
作者:Arwen的异想世界,互联网电商大厂6.5年BI经验;公众号:Arwen的异想世界(ID:Arwendaodaodao)
本文由 @Arwen的异想世界 原创发布于人人都是产品经理,未经许可,禁止转载。
题图来自 Unsplash,基于CC0协议。
收藏已收藏{{ postmeta.bookmark }} 点赞已赞{{ postmeta.postlike }}